From: John Conover <john@email.johncon.com>
Subject: Re: Electronic Components Shipments Industrial Marketplace
Date: Wed, 14 Oct 1998 23:37:47 -0700
John Conover writes:
>
> The model is that duration of the fluctuations in industrial markets
> have a probability of 1 / sqrt (t). It is not complicated. What's the
> probability of a "recession" lasting longer than four months? 1 / sqrt
> (4) = 1 / 2 = 50%. And longer than two months? 1 / sqrt (2) = 0.707 =
> 71%. How about longer than seven months? 1 / sqrt (7) = 0.378 = 38%.
>
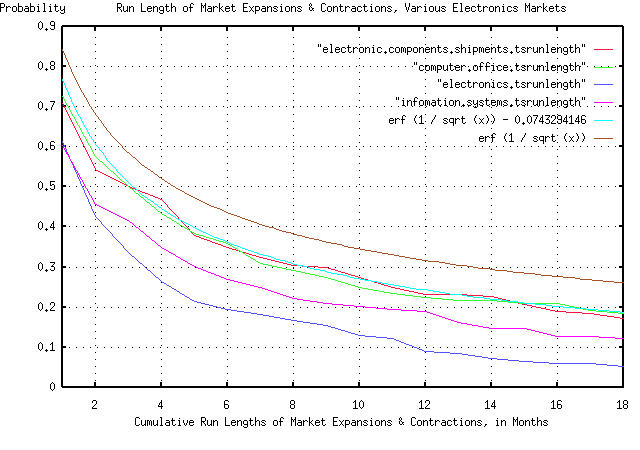
But how well does the model work in other markets? A reasonable
question. So, I used additional data available through the Department
of Commerce, and made a composite overlay graph. The industrial
markets were selected from the electronics industry:
MSEL367X: Electronic Components and Accessories Shipments
1980-1995, by the month.
IP357XXX: Computer & Office Equipment Industrial Production
1982-1995, by the month.
MNELELEC: Total Electronics New Orders 1980-1995, by the month.
MSELINFS: Information Systems Shipments 1979-1994, by the month.
The methodology used to make the graph was identical with the
methodology used in the previous graphs. Again, the graph is
compelling:

As before, all the graph means is that if you want to find the chances
of the duration of an industrial market expansion or contraction being
longer than, say four months, you find 4 on the x axis, move up to the
graph, and left to the y axis, and read about 0.5 = 50%. There are
six graphs displayed. The "real" graph is erf (1 / sqrt (t)), and is
the graph that should be used. The graph erf (1 / sqrt (t)) -
0.0743294146 is what we would expect to see if our data set was 181
months, and the remaining graphs are the empirical data from the
Department of Commerce, which consisted of 181 months, for the various
electronics markets. All in all, a respectable "fit" of empirical data
to our theoretical model, particularly when considering that each
empirical data set consisted of only 181 data points.
So, the assumption that our model of the duration of expansion and
contraction intervals in industrial markets can be calculated as
having a probability of happening of 1 / sqrt (t) seems to be
intuitively justified, irregardless of whether we are talking in
months or years, or any other industrial market.
John
--
John Conover, john@email.johncon.com, http://www.johncon.com/