From: John Conover <john@email.johncon.com>
Subject: Re: Positive & Negative Bubbles in Asian Markets and Re: Noise Trading and the Asian Market "Holes"
Date: 16 Feb 1999 03:20:03 -0000
conover@netcom.com writes:
> Burkhard C. Schipper writes:
> >
> > The weakness of most of the bubble models is that the can not explain
> > edogenously to full satisfaction the how and when the bubble burst.
> >
>
> Hi Burkhard. Depending on you point of view, (and there are many
> POVs-most perfectly defensible,) a probabilistic definition of
> "bubbles" does exist. Although the stochastic POV can not give a
> definite date as to when a a "bubble" will burst, it can give a
> reasonably accurate probability of it continuing into the future.
> That's the relevance of the graphs at:
>
> http://www.johncon.com/john/correspondence/981230002304.31518.html
> http://www.johncon.com/john/correspondence/990212211510.16959.html
>
> The concept of "bubbles" seems to be ubiquitous in economics, for
> example:
>
> http://www.johncon.com/john/correspondence/981014233807.19309.html
>
> is a similar graph for the probabilities of "bubbles" in certain
> industrial markets. GDPs of countries seem to exhibit a similar
> phenomena.
>
> Describing the underlying economic fundamentals and processes that
> would make these graphs the way they are, (which seems to be close to
> a random walk fractal,) appears to be a very difficult undertaking.
>
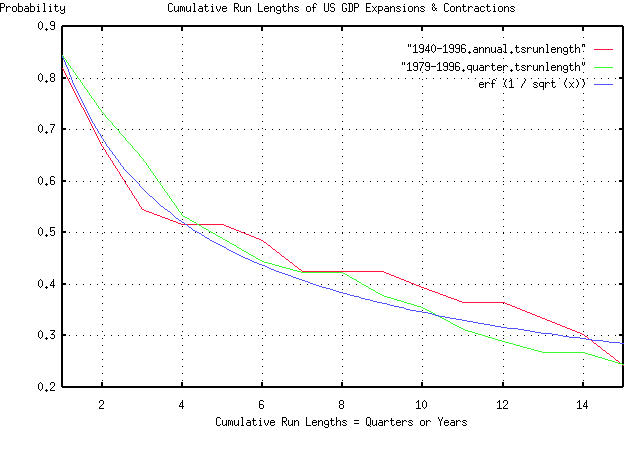
Attached is a graph of the cumulative run lengths of the "bubbles" in
the US GDP from 1940 through 1996, by the year, and 1979 through 1996,
by the quarter. (The data for 1940-1996 came from
http://cher.eda.doc.gov/BudgetFY97/index.html. The data for 1979-1996
came from http://www.stat-usa.gov/.) By comparison, a graph of the
function erf (1 / sqrt (t)) is provided, which is the theoretical
cumulative run lengths of a random walk fractal.
Interestingly, with only 56 and 72 data points, respectively, the
probabilities of the run lengths seem to be asserting their self as
identical to a random walk fractal-although these methodologies favor
large data set sizes. (Additionally, note the self-similarity, ie.,
the "bubble" run length probabilities are independent of the time
scale used-the hallmark of a fractal system.)
John

-- John Conover, john@email.johncon.com, http://www.johncon.com/